ELECTRO-VORTEX FLOW IN LMBs

From 2018 to 2020, we have studied on electro-vortex flows in liquid metal batteries. It is possible to drive fairly intense flows, in particular in the case of swirling electro-vortex flows. We have studied wheter these flows can be detrimental or on the contrary, useful to improve LMBs.

Multiphase simulation of electro-vortex flows

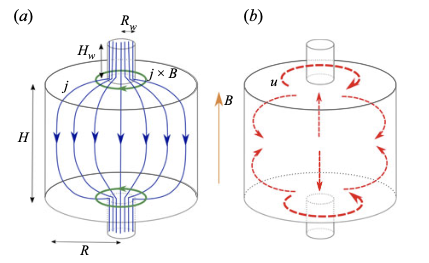
We started our investigation of electro-vortex flow in a hypothetical three-layer LMB, that connects to two solid thinner electrodes (- and +) at the top and bottom. During discharge, we can then have the following situation

In the middle plot, we sketch lines of electrical current (in red) that spread out into the liquid metals at the top (-  pole) and converge back to exit through the bottom (+ pole). As a result of this curvature in the current lines, we get a non-zero Lorentz-force that can not entirely be balanced by pressure gradients. The remaining, effective part of the Lorentz force pushes the metal along the thick blue lines. This creates jets of liquid metal that push fluid away from the wires and recirculate along the thick green paths in the right panel. When sufficiently intense, we expect that this flow can locally compress the electrolyte near the axis. In that case, electro-vortex flow might cause a undesirale short-circuits in a LMB. 

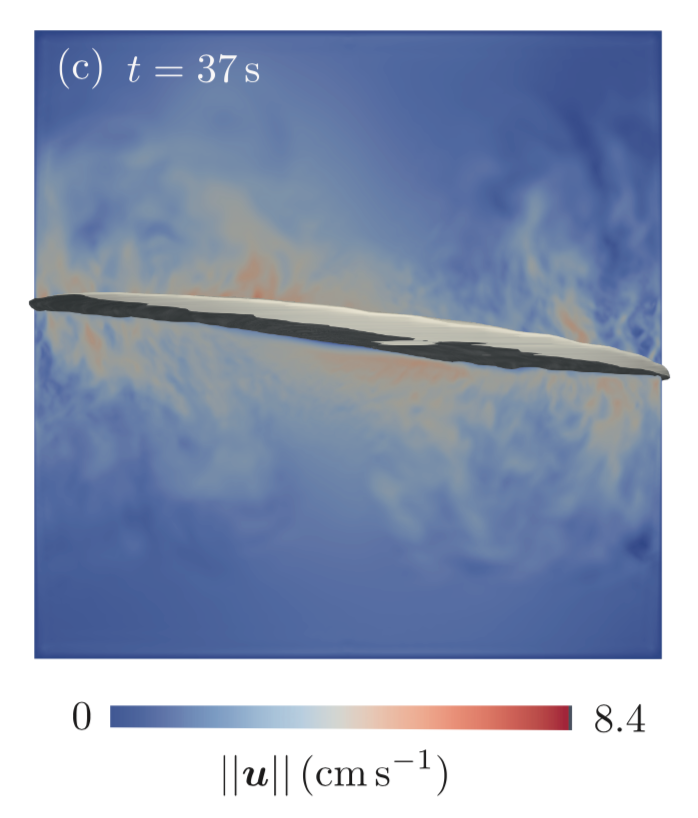
In our first article on electro-vortex flow, we have done numerical simulations of these electro-vortex flows in one, two and three-layer set-ups. Here is a picture of an axisymmetric  multiphase simulation in a Mg-Sb liquid metal battery of fairly small size (cm range). The following images, result from a simulating of a short-circuit triggerd by electro-vortex flow in a Mg-Sb LMB. We show snapshots of the flow intensity in a meridional plane  (r-z) plots at successive times

An intense jet blows the top metal downwards near the axis. This creates a bulge in the salt layer that splashes up and for a short amount of time we observed a short circuit. To get this flow induced short-circuit in this small cm-scale cell, we needed to use electrical current densities that are unrealistically high, but the same phenomenon would be possible with lower, realistic current densities and in larger cells. 

As in our Tayler instability article, we find that a simple energy balance can be used to correlate the observed interface deformation (eta_max) with the flow’s intensity (U_max)

Using the principle of similitude and assuming that the height of the electrolyte layer does not influence the strength of the electro-vortex flow and the interface deformation, we can rescale our simulations to other similar set-up and estimate under which conditions electro-vortex flows may cause short-circuits. The following figure shows the expected interface deformation (eta_max) as a function of the radius R of the cell and for various scenarios of electrical current density

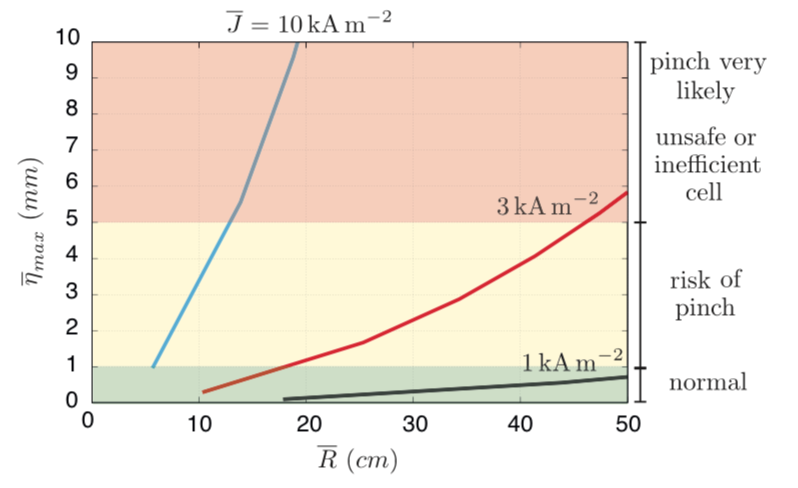
We compare this typical interface deformation to the typical electrolyte layer height that is expected to range in 1-5 mm. This allows to delimit three regions: in the green region the expected interface deformation is smaller than 1mm so a pinch unlikely. In the yellow band, there is a risk of pinch as the expected interface deformation is between 1 and 5 mm. In the red band, it is fairly certain that the flow is sufficiently intense to pinch trhough the electrolyte, plausibly for prolonged amounts of time.  

Given that present day Mg-Sb LMB prototypes have current densities (near the electrolyte) that culminate at J = 3kA/m^2 we estimate that the red line delimits the maximal deformation. This suggests that electro-vortex flow can be sufficiently intense to pinch electrolyte layers in batteries with radii of around 15 to 45 cm (and with the suposed wiring). Compared to the Tayler instability, the electro-vortex flow clearly is more intense and it may cause short-circuits in moderate size cells. 

Our article was published in 2019 in PRF and is here available as a preprint. Most results were obtained during the internship of P. Ziebell Ramos.

Electro-vortex flow as a mixer ? 

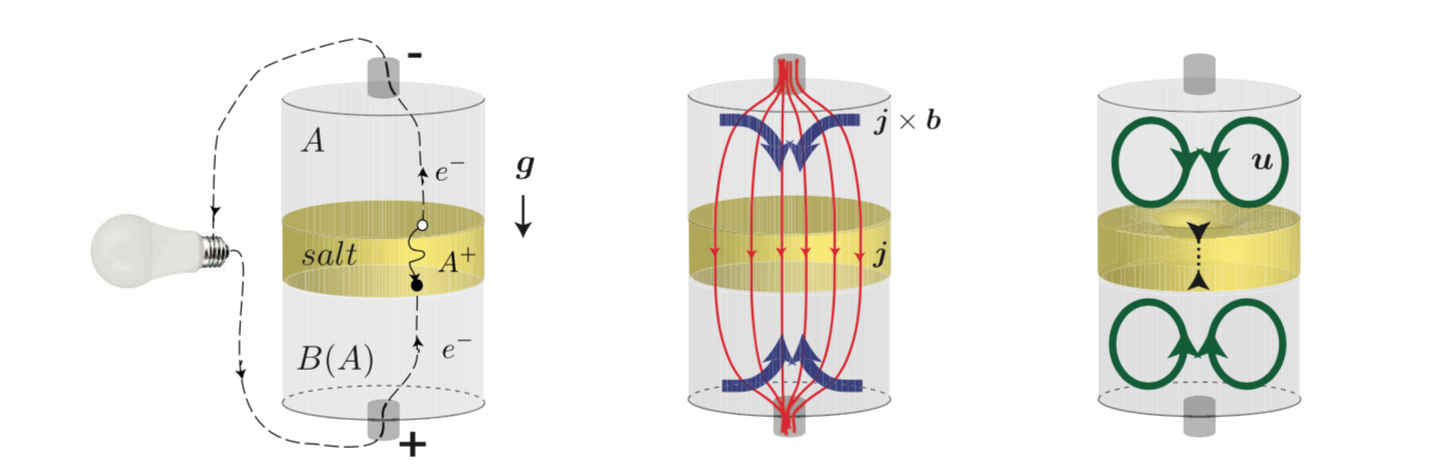
Most initial studies on flows in LMBs saw flows as potentially harmful to the battery, but flows may also be useful to improve LMBs. As shown in the sketch below (a) and (b), discharge is accompanied by a downwards mass flux of light element (here Li). This light material enters the top of alloy layer (here Pb(Li)) the bottom layer of the LMB and mixes into the alloy by diffusion. Since this binary diffusion is rather weak, a local accumulation of light element may be created when discharging rapidly as in panel (b) below

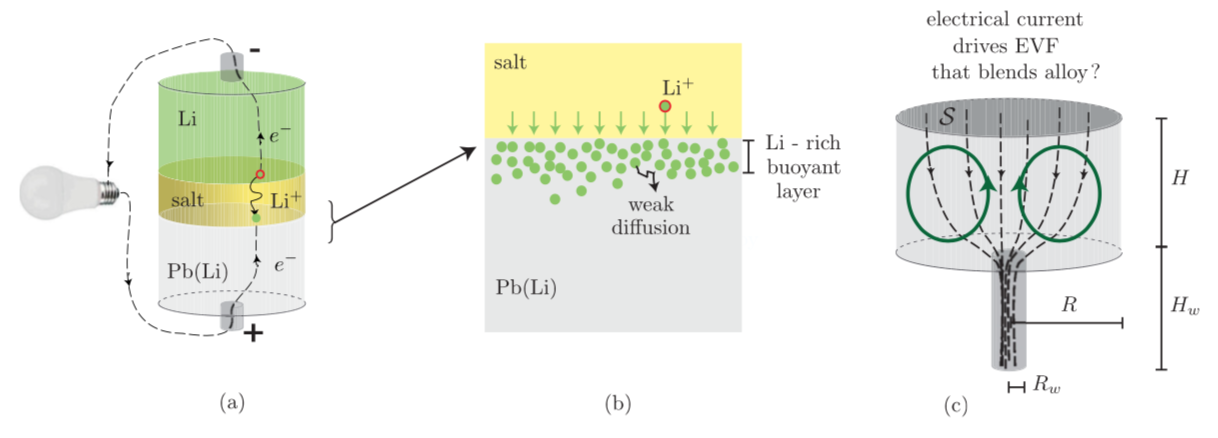
The formation of such a inhomogenous layer, concentrated in light element is not good news for the battery: the electrical potential of the cell drops and so does the delivered power. Furthermore, there is a risk that solid intermetallic phases start to grow in this layer, which further block transport. During charge, the inverse takes place: light material is evacuated from the alloy that may become locally depleted if charging too quickly. This also has a negative effect on the battery efficiency.

In the line of several other research groups, we have investigated whether electro-vortex flows could be usefull to enhance the mixing of the alloy and to prevent this type of strong inhomogeneity. 

In our first article on this subject, we used a Boussinesq model to simulate the flow and varying composition of the bottom layer alloy. Motion is induced by the electro-vortex mechanism as this layer is electrically connected to a thinner solid electrode from below. Electro-vortex flows should drives a upward jet in the alloy, as shown by the green lines in panel (c). A permanent, constant flux of light element comes from the top and this flux is proportional to the current density (for each elementary charge that is passed one Li atom enter the alloy). We invesitigate how and if this electro-flow mixes the alloy during discharge and charge.     

To describe this binary alloy dynamics, you need detailed information on the material properties of a typical alloy. This information was provided to us by P. Personnettaz (HZDR) during a short visit at LIMSI, spring 2018. As in his study, we choose for Pb(Li) alloys since material properties are well known (this alloy is planned to be used in tritium breeders around fusion reactors). The following plot shows how the density of the Pb(Li) alloy at T = 500°C, varies with mass concentration of lithium (rho_Li) or molar fraction (x_Li). From left to right, the alloy varies from the eutectic composition (molar fraction x_Li = 17%) up until an alloy that is so concentrated in Li (x_Li = 60%) that it solidifies. 

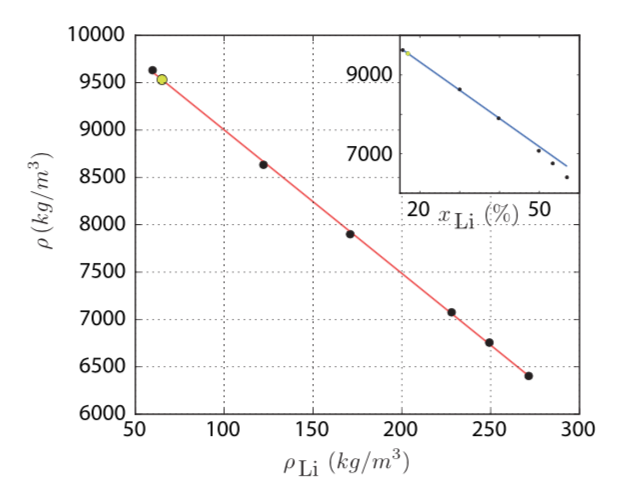
Obviously, the change in density is just huge, ranging some 3000 kg/m^3. This suggests that solutal buoyancy effects, i.e. local changes in density due to changes in composition, will actively act on the flow through Archimedes forces. Prior to Personnettaz et al. 2018 work, not a single study on flows in LMBs has taken this aspect into account, the alloy in the bottom of LMBs certainly is not one of constant density. 

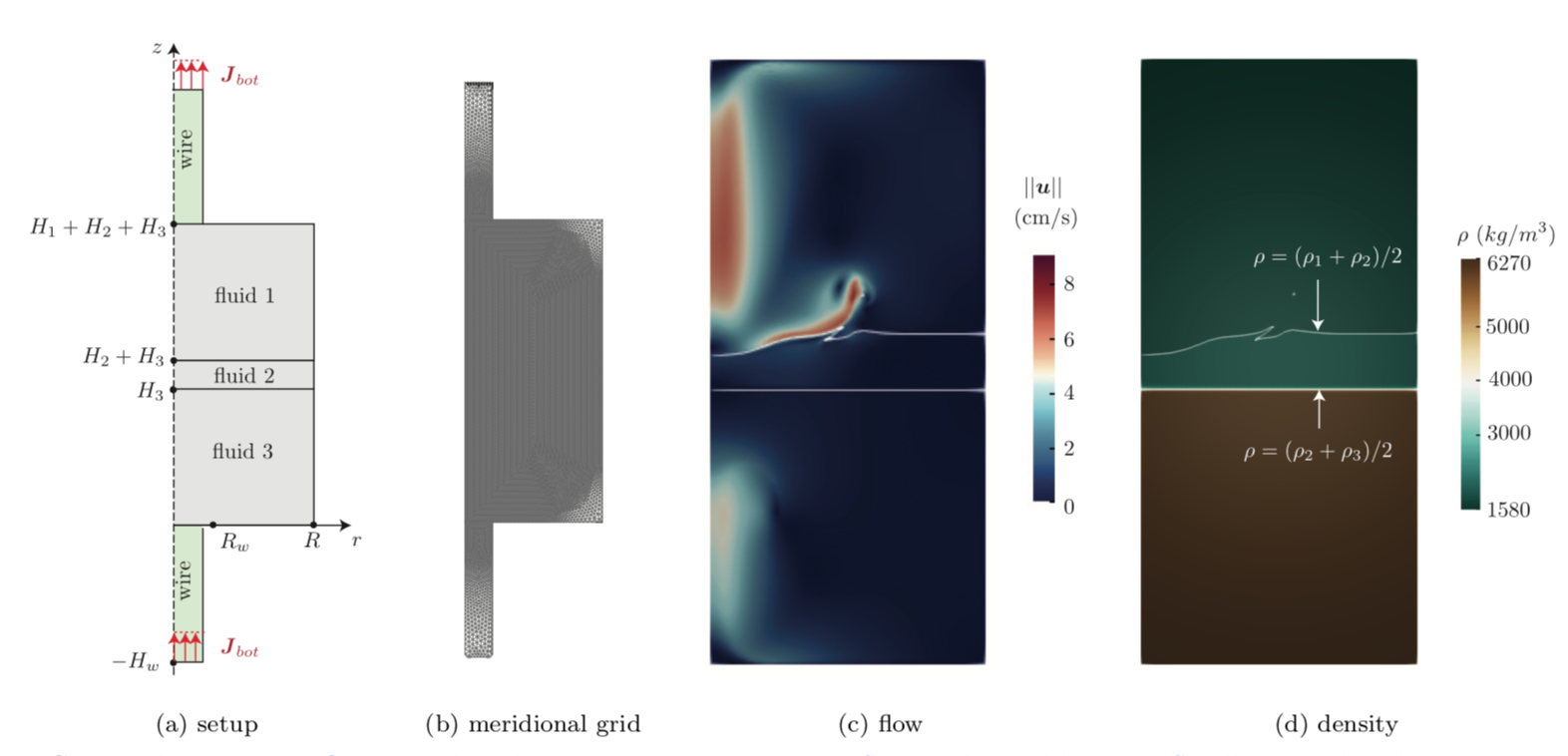
In our simulations, we demonstrate how solutal buoyancy effects, indeed have a drastic impact on the flow in the bottom layer. If we wrongfully ignore solutal buoyancy, we observe that the electro-vortex flow affect the mixing in the alloy. On the left, we show the flow in vertical planes for a high discharge current density in a cm scale cell. On the right, we show the molar fraction x_Li the alloy. 

The electro-vortex flow clearly seems to affect the molar fraction and seemingly enhances mixing. However, if we take into account solutal buoyancy for a realistic gravity, the top layer alloy righ in Li also becomes lighter. This creates a stabilizing density stratification, at the top of the alloy that simply floats on bulk alloy. The electro-vortex flow in the bulk never succeeds in reach through that stagnant buoyant layer and  never enhances mixing. This can be seen in the following series of snapshots, for the same discharge current density of 5000 A/m^2 (colour = molar fraction, streamlines of flow). 

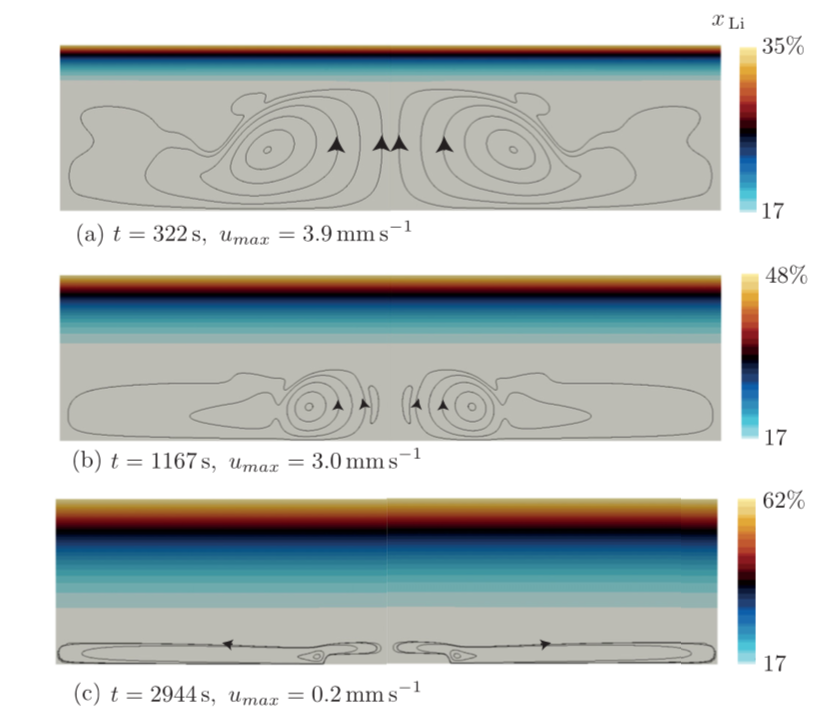
This just suggests that solutal buoyancy is huge and that it is quite efficient in preventing enhanced mixing during discharge.

To have a better view on what magnitude of flow really is required to have enhanced mixing, to prevent this stabilising stratification, we have derived a physical model. As time passes, a diffusive front of width sqrt(Dt) moves into the alloy at the top making it locally lighter. Depending on the intensity of flow in the bulk, we can imagine different scenarios:

Pushing a heavier bulk fluid particle through lighter top alloy, requires a minimal amount of work. This work can be delivered by the bulk flow, if it has enough kinetic energy available. A too weak flow cannot push through the stable stratification and will not effect mixing, a strong flow can blow the stratification away and hence enhance mixing.

To estimate the mixing capability of a flow, we need to compare its intensity U to two characterstic velocity scales U_p and U_m, with the following physical meaning. In a cell of height H a flow of intensity U requires at least an advective time t_a = H/U to devellop. During this time a minimal, non-avoidable stable stratification will build up at the top of the alloy. From simple energy balances (kinetic <-> potential) we can calculate a minimal flow intensity U_p to push through the minimal stratified layer and a minimal flow intensity U_m to transport lighter fluid parcels all around the cell, against the stabilising buoyancy. Schematically:

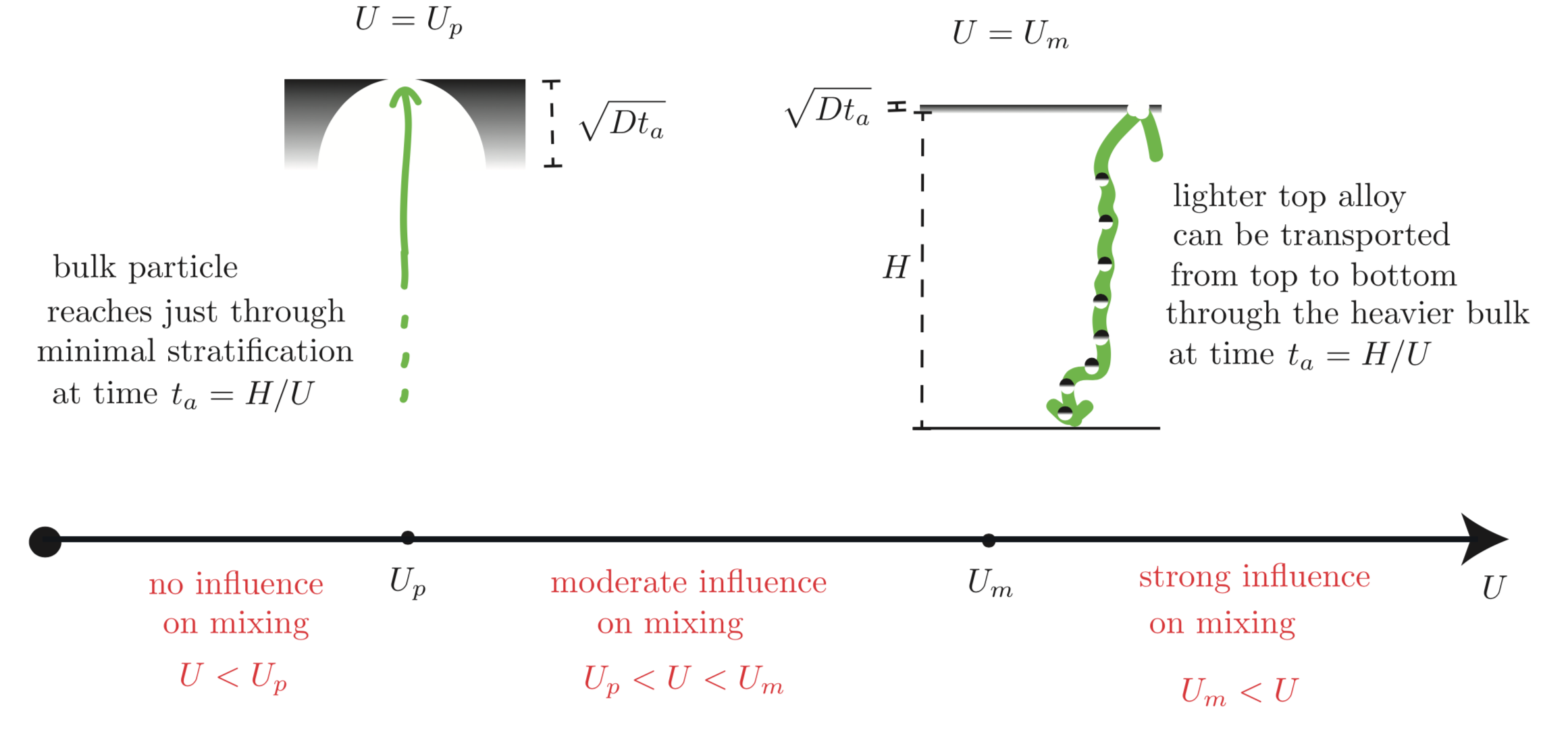
A too weak flow with intensity U < U_p will never reach through the minimal stratified layer and hence never affects mixing. A strong flow, with intensity U > U_m has the capacity to prevent a strongly stratified layer as it can very quickly redisctibute light fluid parcels all around the bulk alloy. In between, for U_p < U < U_m, we have a moderate effect of the flow and enhanced mixing possibly occurs only for a finite amount of time. 

The precise expressions of U_p and U_m only depend on input and material parameters. We find  

and

where J is the imposed current density, M_Li the molar mass of lithium, beta the solutal expansion coefficient, g gravity, H the height of the cell, n_e = 1 the number of charges carried by the transported Li-ions and F is the Faraday constant. D is the binary diffusion coefficient of the alloy.

In the article we have tested the pertinence of these velocity scales in the mixing process, using simulations under micro-gravity. Combined with scaling laws for the intensity U of flows, we can use these criteria to figure out which flows can be useful to enhance mixing in LMBs and , under which conditions. For our own simulations of discharge with real gravity, we found  U<U_p always, in agreement with our observation of the formation of a stagnant buoyant (unmixed) layer. 

During charge, the role of solutal buoyancy is as large, but destabilising. As the alloy gets locally heavier at the top, a solutal convection flow is quickly driven in the alloy. This flow totally overpowers the electro-vortex flow and will always mix the alloy very well. During charge, solutal buoyancy naturally prevents inhomogenity in the alloy. In the article, we have done some challenging three-dimensional simulations of this solutal convection flow. The following snapshots show the molar fraction inside a cell that is being charged at low rate at different times

Using theoretical arguments, we have been able to derive scaling laws for the intensity of this convective flow, for the mixing time and remaining inhomogeneity in the alloy.

This work was published in PRF in 2020. A preprint is available here. Most results were obtained during the internship of S. Bénard, that is now doing here Phd in our group (joint supervision with C. Nore).  

Swirling electro-vortex flow

In both our previous studies, we investigated electro-vortex flow in the absence of background magnetic fields, but in many situations there is a non-zero background field. This extra magnetic field has a strong impact on the electro-vortex flow and may cause a rapid swirl. We investigated whether this swirling electro-vortex flow is intense enough to oppose solutal buoyancy in our idealized battery. 

The following sketch shows the investigated set-up. As in the previous study, we focsus on the alloy layer. The only difference is that there is a homogenous vertical magnetic field ‘’en plus’’. 

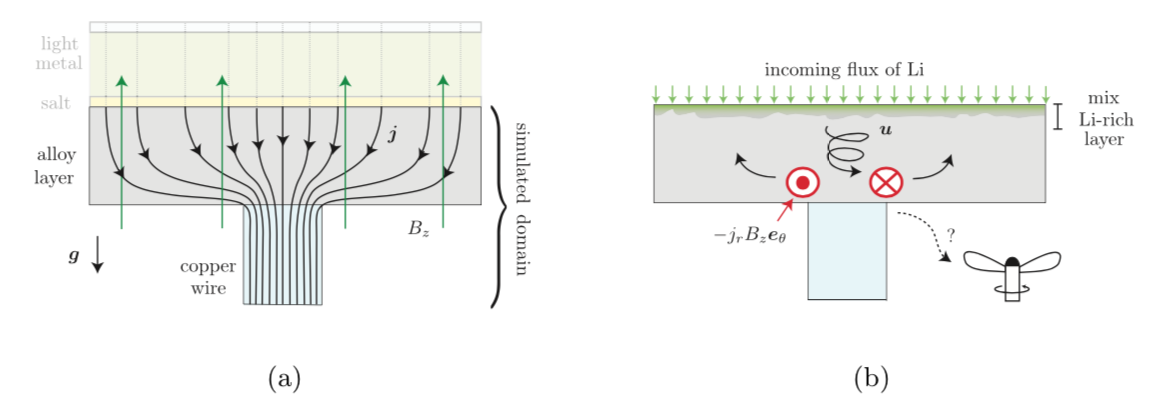
Due the vertical magnetic field, the Lorentz-force has a component that is azimuthal and localized near the electrical contact, where j_r is largest (singular). This azimuthal forcing creates a swirling flow and since forcing mainly occurs at the bottom, we can compare this forcing to what we have in a ‘’blender’’ with rotating propeller in the bottom. The expected flow is one that spirals downwards near the axis and recirculates off axis. This is a snapshot from a challenging 3D-simulation of the molar fraction of lithium the alloy, in a rapidly discharged battery.

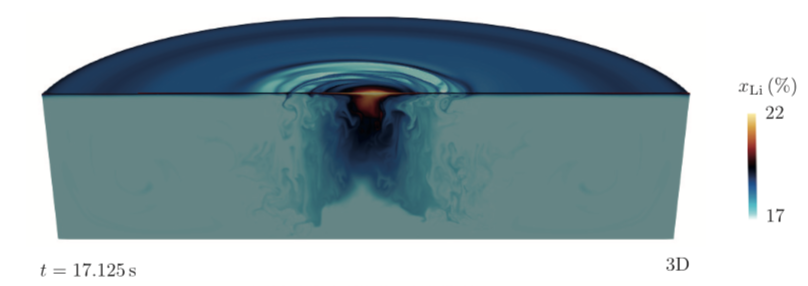
We clearly observe the impact of the swirl and also how lighter alloy is being dragged into the alloy. Where non-swirling electro-vortex could not could an efficient mixing, we observe that swirling electro-vortex flows can. In relation to the mixing criteria of our previous work, we find indeed that the flow intensity is above U_m, threshold for efficient mixing. 

In the article, we provide further insights in the flow physics. We show that the swirling electro-vortex flow intensity is governed by a scaling law 

where J is the current density at the top of the alloy, B_z the imposed magnetic field, rho_* the density of the bulk alloy, R the radius of the cell and nu, the kinematic viscosity. In combination with the criterium for enhanced mixing U > U_m, we can propose a formula to estimate the minimal magnetic field needed to enhance mixing in LMBs.  

Von-Karman-like swirling electro-vortex flow

The 2/3 scaling law that we observed in the simulations of swirling electrovortex flows was unknown to us at that time and also unexpected. A very simple balance of inertia and Lorentz force rather suggests a scaling law 

Why do we osberve a different scaling law ? This question motivated us to do a more detailed on the electrovortex flow itself, disconnected from the liquid metal battery context. What are the different scaling regimes of electrovortex flows as we crank up the Lorentz force? This question was given to Sabrina Bénard, who started her Phd in our group in 2020. 

We consider a column of liquid metal connect to two thin electrodes on the top and bottom plates. The whole cell is in a weak uniform vertical magnetic field. Applying a potential difference between the top and bottom, wire electrodes, an electral current will run through the cell. Near the electtrical contact, we expect a non-zero Lorentz force that will drive a flow that bares many similarities with the Von-Karman flow that can be driven using counter-rotating impellers. Interestingly, there are no rotating boundaries here: all the walls are static

We simulate the flow for changing imposed magnetic field and current density. We study the structure of the flow and how its intensity varies. … (to be continued)