METAL PAD ROLL INSTABILITY

In the Tayler instability study we only considered a battery as a layered fluid system that is being traversed by a vertical electrical current. But whenever there also is a small ambient background magnetic field present, we can have an entirely different source of motion: the metal pad roll (MPR) instability. Gravity waves are electromagnetically amplified and may spontaneously grow on the interfaces between superimposed layers.

MPR basics

The metal pad roll instability is a very well known phenomenon in the Aluminium industry as it is known to occur in Hall-Heroult reduction cells. These cells are used to fabricate Aluminium on large scale and they are conceptually similar to liquid metal batteries. A typical, simplified sketch for one reduction cell is 

Hall-Heroult cells are very shallow cells (typically a few meters in lateral size, but only 30-40 cm high) with only two layers of fluid. The top (lighter) layer is the badly conducting cryolite (a molten salt at 1000 degrees Celsius that dissolves alumina). The bottom layer is molten aluminium. During the reduction process, vast amounts of electricity are consumed to reduce Aluminium from the alumina in the cryolite and to keep the system heated. The oxygen liberated by the reduction reacts with the carbon anode blocks that gradually consume into carbondioxyde. 

A typical Aluminium factory has a elongated shape, with a vast amount of such Hall-Heroult cells (green rectangles in sketch) organised around a central current loop (dashed line).

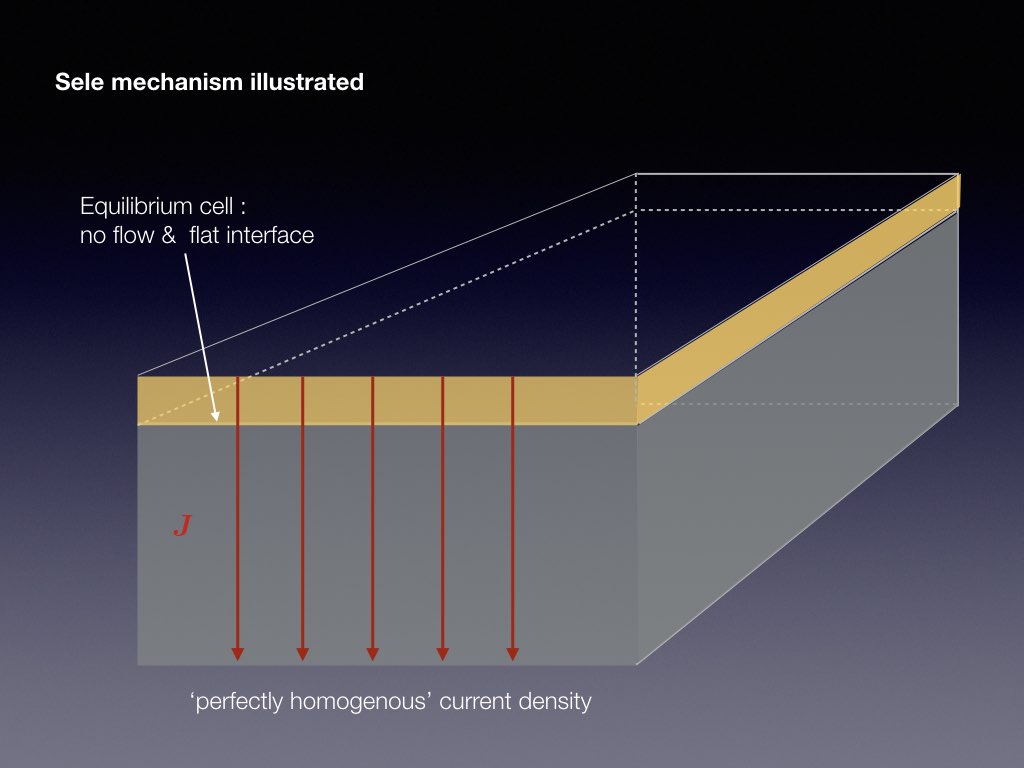
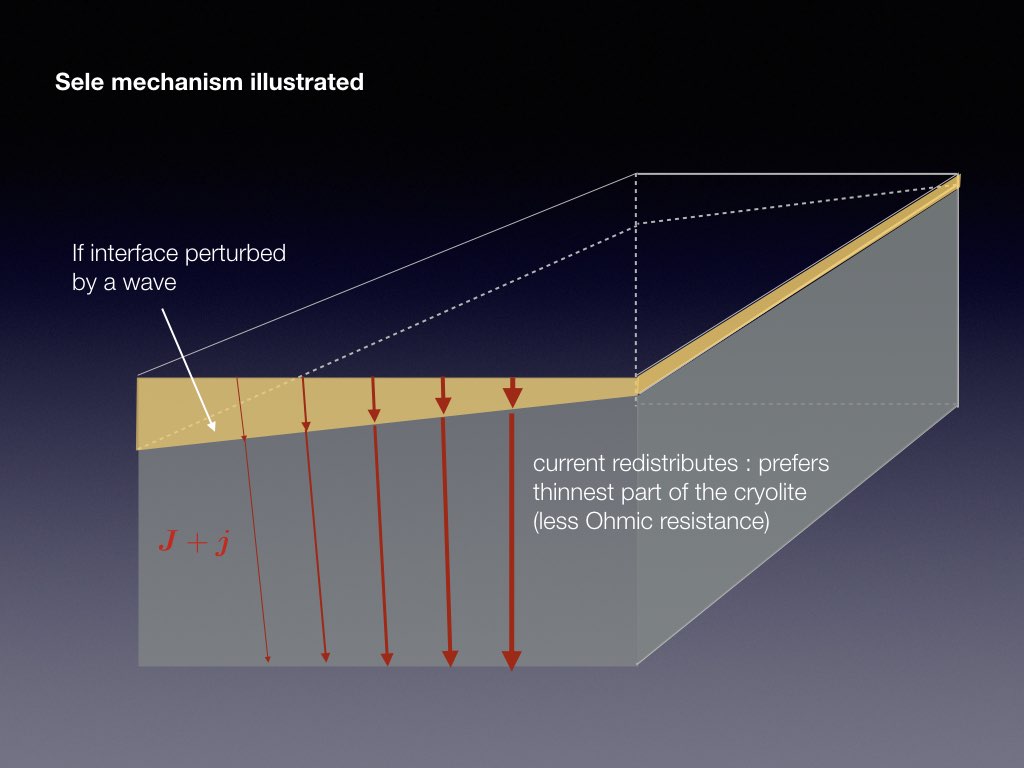
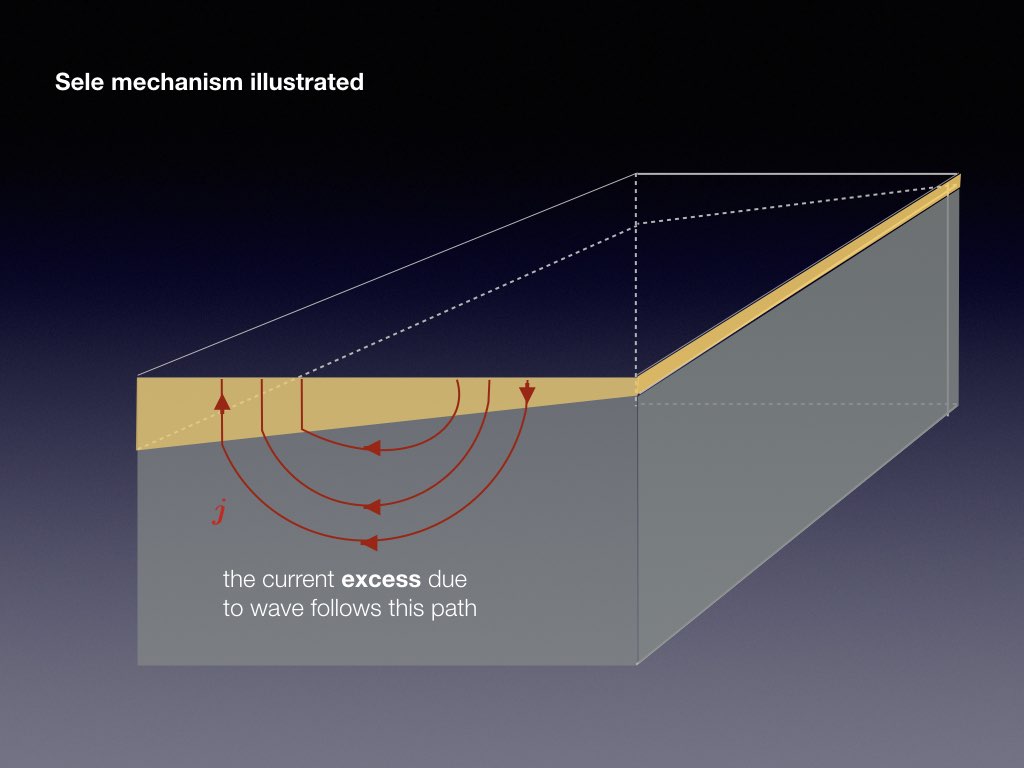
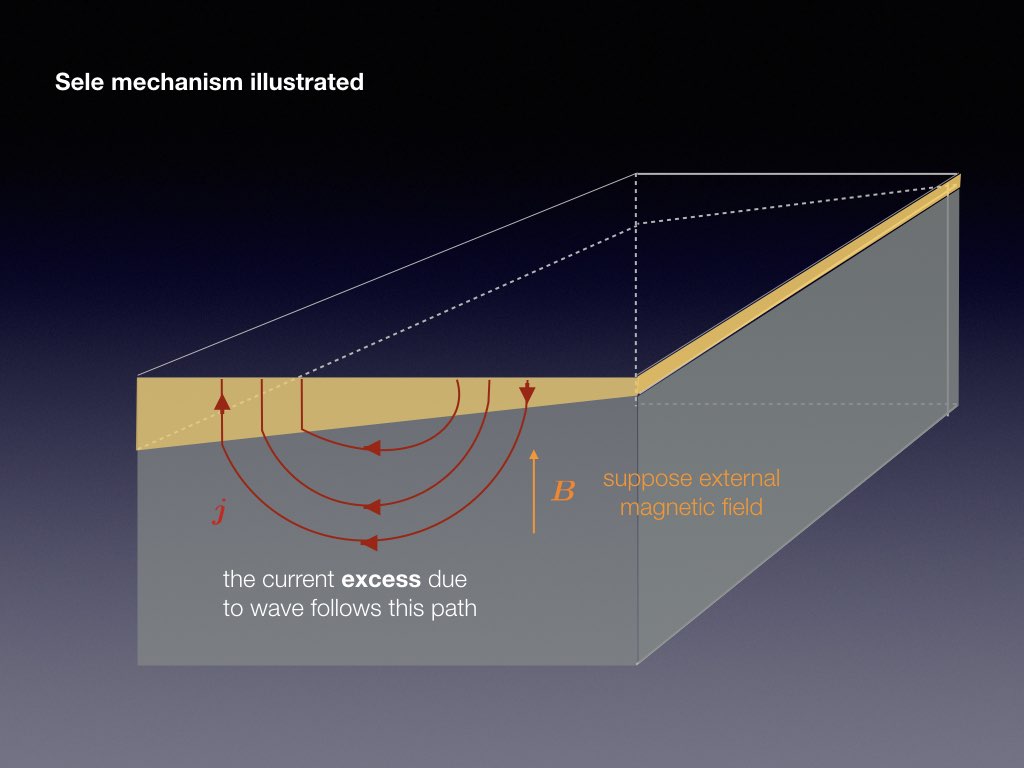
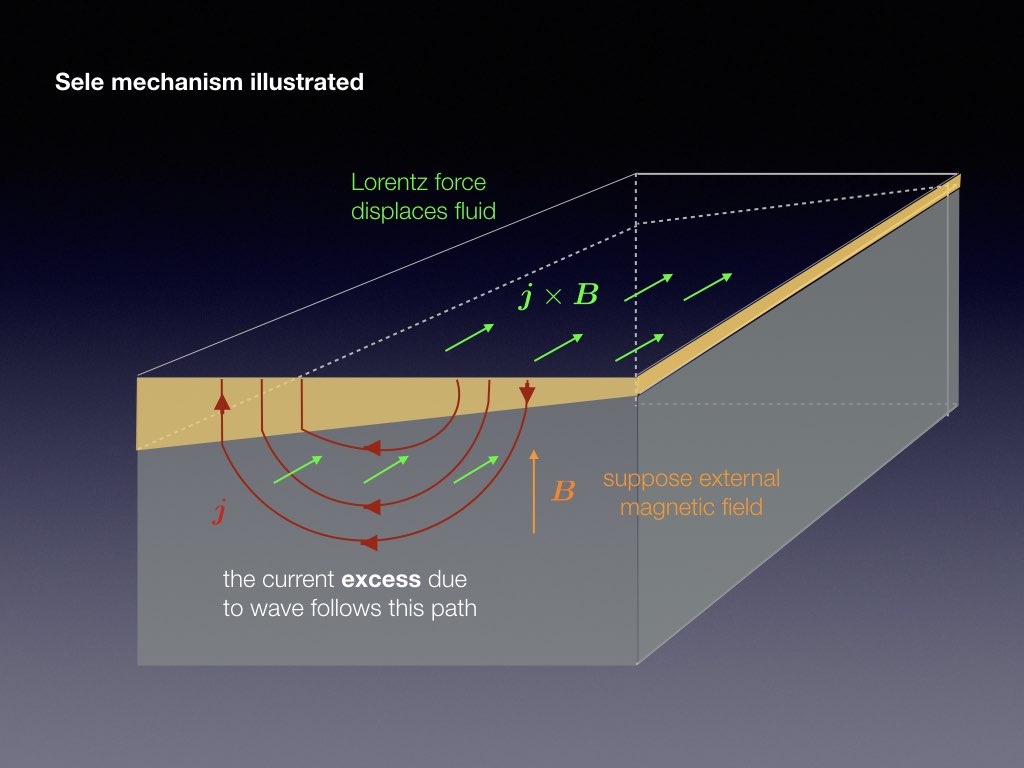
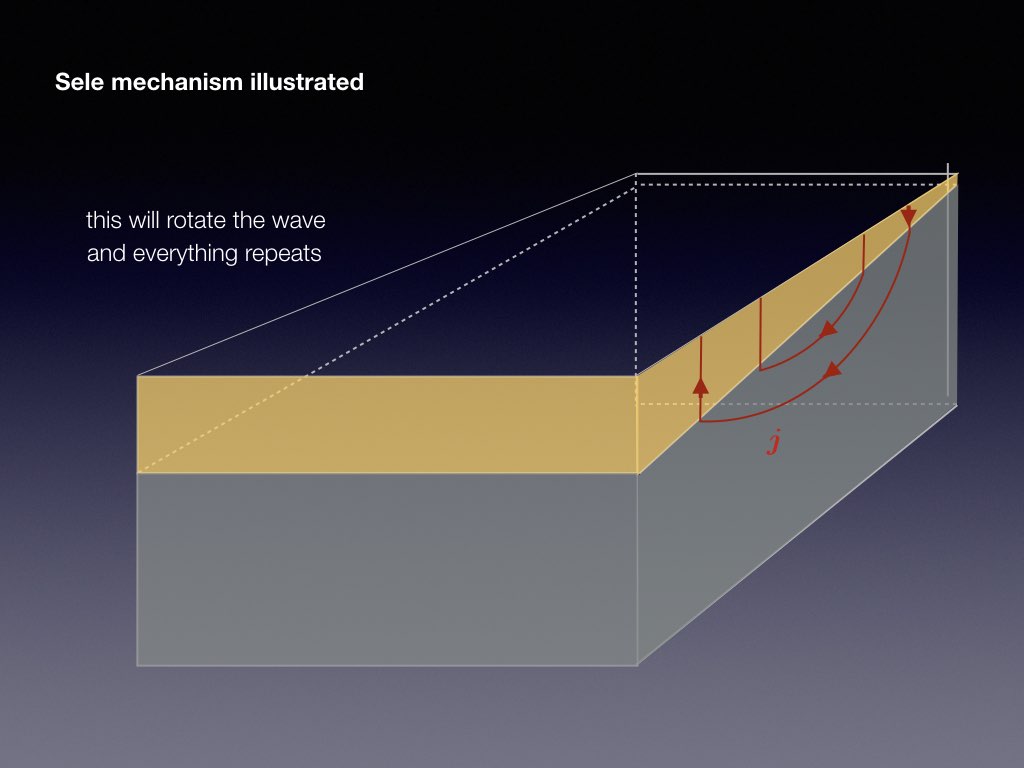
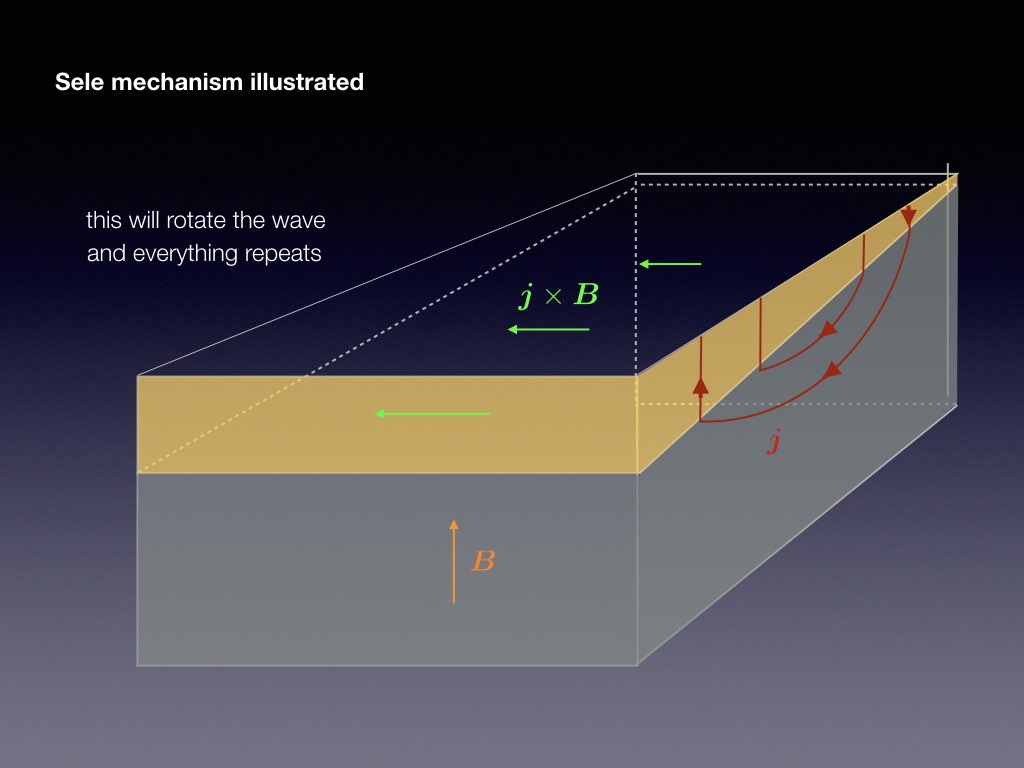
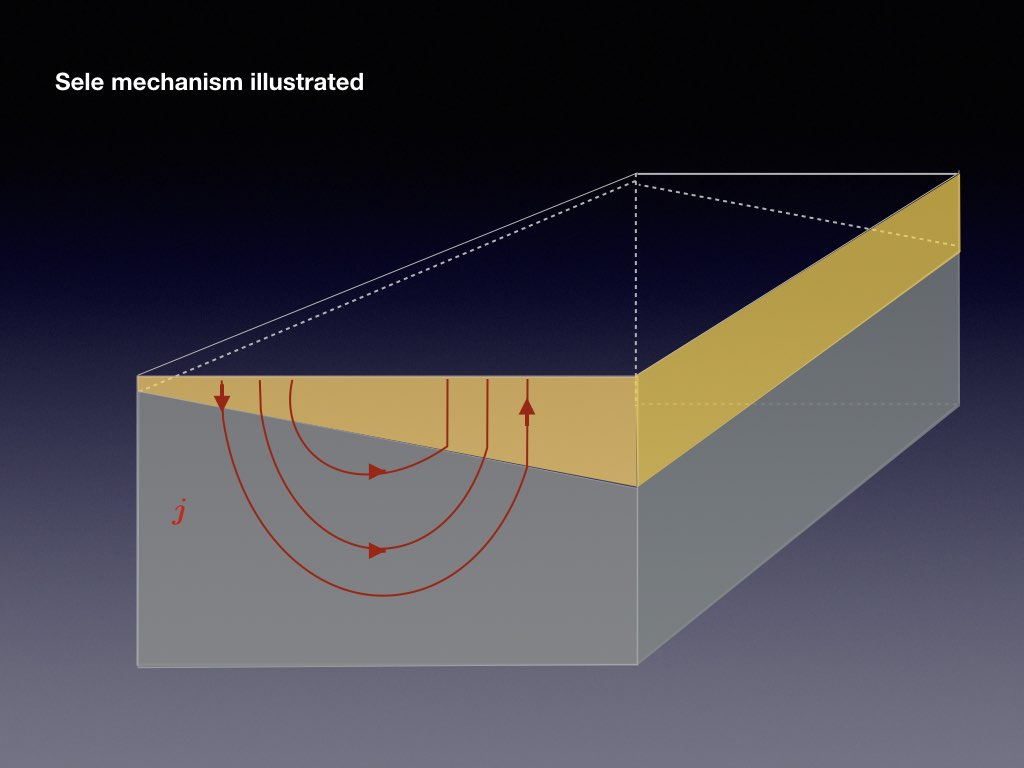
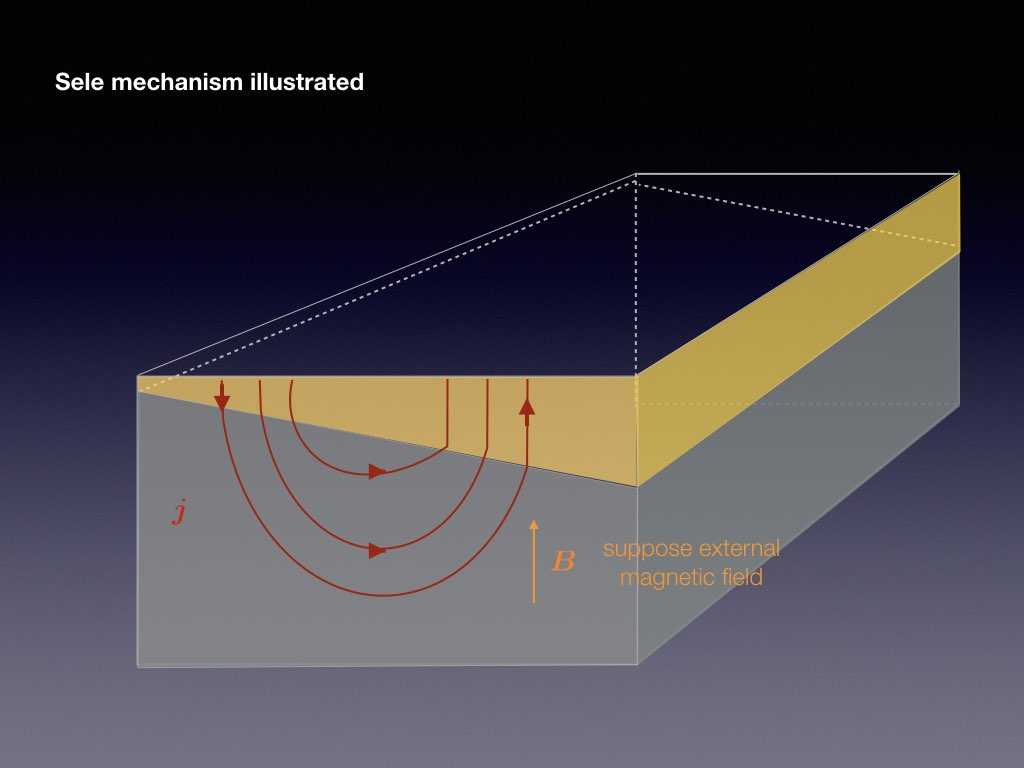
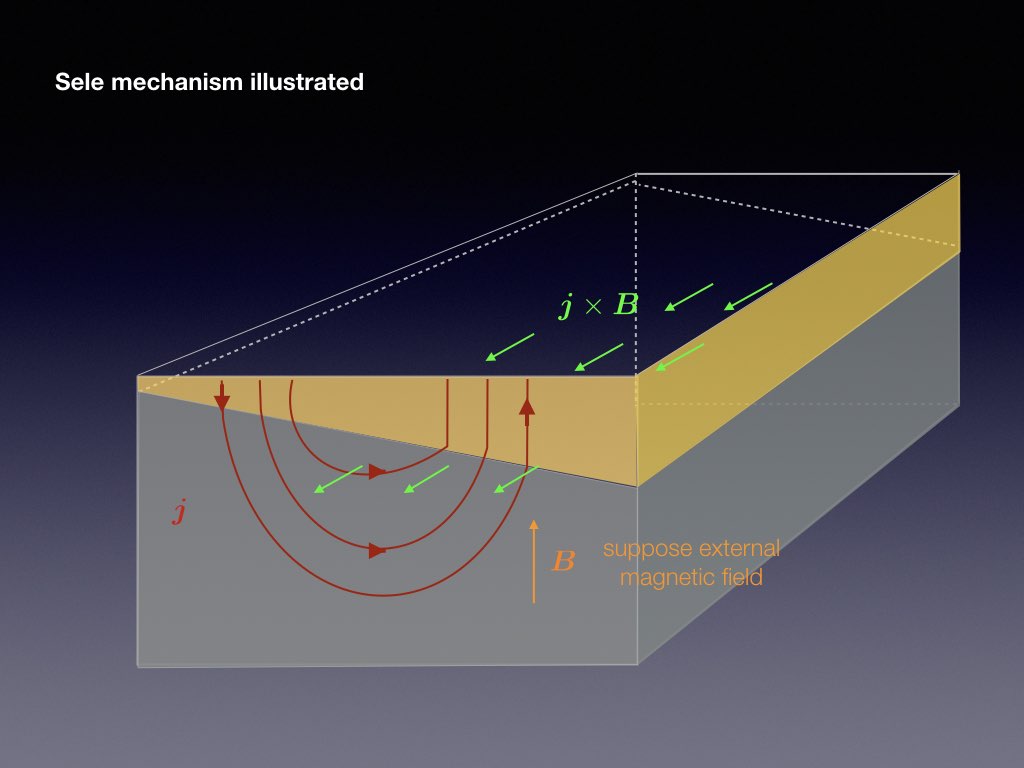
Electrical currents through each cell and through the factory reach intensities of more than 100kA. This causes a ambient magnetic field that has a typical magnitude of a few mT. It is the combination of the vertical magnetic field component of this ambient field with the reduction current that destabilises the interface between the aluminium and cryolite. The following slide-show explains the basic physics of the Sele  instability mechanism

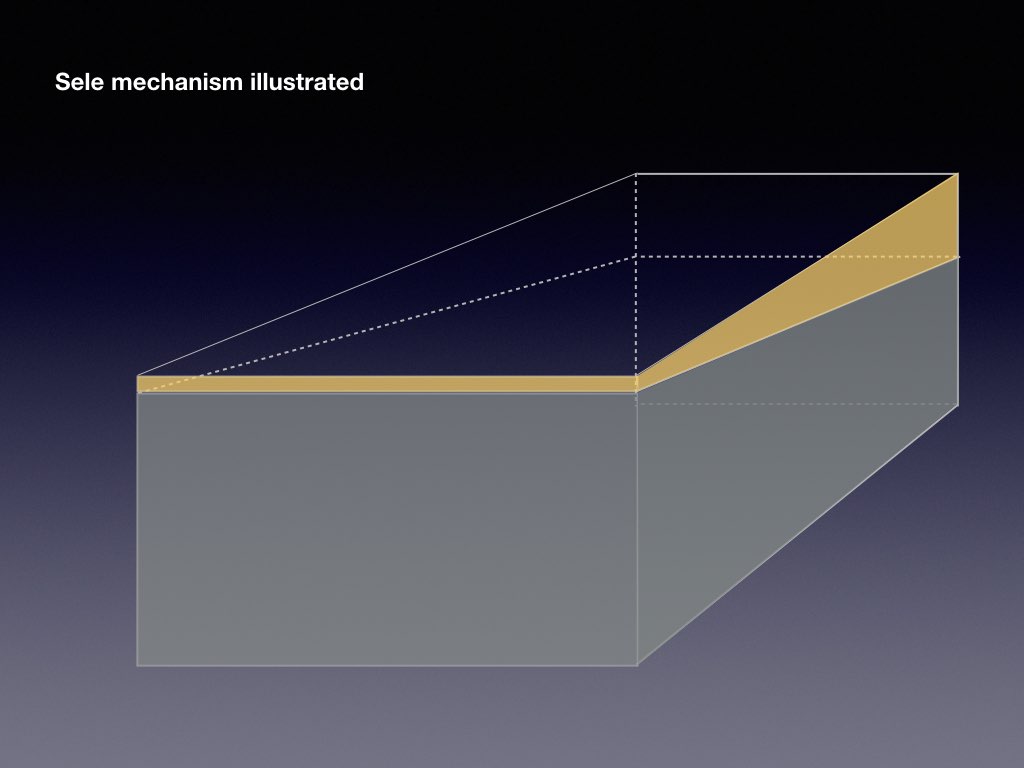
The presence of a jump in electrical conductivity is essential to the metal pad roll instability as otherwise, the electrical current would not redistribute when a wave occurs on the interface. Another essential ingredient, not present in the previous sketch, is that transverse standing waves need to couple efficiently:

When the electromagnetic coupling is weak, metal pad roll instability can be seen as a parametric resonance phenomenon, in which standing transverse waves destabilize in pairs, to give, for example, a rotating wave. Resonant coupling occurs when eigenfrequencies of transverse waves are close. In practice, we can always find multiple pairs of waves with close frequencies for any cell with any geometry. Instability criteria are typically expressed in terms of  a non-dimensional number beta and take the shape of

In beta, we recognize I the total current, Bz the vertical ambient magnetic field, the density difference, gravity and the heights of both layers. The geometry of the cell has a direct impact on the difference in frequency of coupled waves and thus affects the dissipationless value of the critical threshold value beta_c, for instability. Dissipation can be due to various sources (viscosity, baffles, turbulence, Joule damping, ...) and always increases the critical value of beta for a pair of waves to be destabilized.

In practice, one can prevent the MPR instability by keeping beta below the critical value. This can be done by decreasing the vertical field component through the design of current wiring around HH-cells, or alternatively, by keeping the fluid layers thick enough. This last option causes however increased Joule-losses and when already 3% of the worlds electricity is being consumed by Al-reduction factories this is perhaps less viable.   

Metal pad roll in liquid metal batteries (2017)

In 2017, N. Weber (HZDR) published two articles on the (multiphase) numerical simulation of metal pad roll instability in cylindrical liquid metal batteries on which we collaborated. In these simulations, we considered a small Mg-Sb liquid metal battery (cm range) carrying a fairly large current density (J = 10-15 kA/m^2) and bathing in quite large ambient magnetic fields (Bz = 10 mT). A typical outcome of these simulation done using OpenFOAM is 

Here is a link to the journal article (Physics of Fluids) or to an arXiv preprint  On the top interface, separating the electrolyte from the Mg-layer, a rotating bulge appears. The deformation is big, mainly because the density difference between the Mg and the molten salt is small (~138 kg/m^3). The bottom interface, between the electrolyte and the bottom Sb(Mg) alloy is practically undeformed, because the density differency between the salt and the alloy is huge (4555 kg/m^3). 

N. Weber did many simulations, varying most physical parameters (current density, magnetic field, conductivity, …) and in order to get quantitive insights on what is necessary for the cell to become unstable.

Personally, this study made me realize that we had so little theory that could be quantitively compared to these simulations. Almost all available theory was dedicated to shallow cells and dissipative effects were often considered as of secondary importance. The cell simulated here was non-shallow, influenced by viscous dissipation and possibly influenced by magnetic damping. There was just no theory that could be compared to these direct numerical simulations. 

Inspecting the literature on metal pad roll theory, there is an evident time-gap between the theory (last devellopments around 2001) and the direct numerical simulations of the full three-dimensional flow (starts around 2003 in multiple groups). As a result, both approaches, theoretical and numerical, seemingly live in separate worlds. Perhaps it could be possible to design a precise theoretical model for cells that can withstand a quantitive comparison with direct numerical simulations. 

This was the start of a research project on metal pad roll instability, in which I was involved for quite some time. 

Perturbation theory for metal pad roll in cylindrical reduction cells (2017-2019) 

Ever since my Phd, I have been fond of cylindrical coordinates, perturbation methods and waves. This problem of metal pad roll instability in cylindrical cells is just another system in which I could put these skills into practice. The worst is that I could have known form start that this would end up in a very lengthy article, that would take months to write and months to pass review.

The study is now published, either in preprint format or nicely put together by the hardworking typesetters of JFM. 

Cylindrical Hall-Heroult reduction cells certainly do not exist in reality, so I would not call our study realistic. It is a purely academical study that aims to find a matching ground between theory and direct numerical simulations. In the low-beta and low-viscosity regime, one can calculate the growth rates and frequency shift of rotating gravity waves, 1) in cells that are not necessarily shallow, 2) including viscous dissipation, 3) including magnetic dissipation, 4) including capillary effects, 5) in fluids with arbitrary conductivities. The studied cell looks as

with fluid 1 on top and fluid 2 in the bottom, with density, conductivity and kinematic viscosity (rho,sigma,nu). Inviscid potential waves can exist on the interface between both fluids. Each wave is caracterized by and azimuthal wave-number m and a radial wavenumber k and the frequency is set by the dispersion relation

here gamma_1|2 is the surface tension of the interface.  We calculated the growth rate of a given wave using a 4-term formula

The first term, lambda_v, is the only potentially destabilising term that can be calculated with a magneto-static and inviscid approximation. This part of the growth rate is the one that is usually calculated in the available metal pad roll  literature. Next to this, we also calculate the quasi-static field corrections lambda_vv and lambda_hh. When the imposed vertical magnetic field is large, lambda_vv captures the magnetic damping due to Joule dissipation of induced currents in the lower aluminium layer (similar to magnetic braking).  The term lamda_hh is  always very small and due to the horizontal (azimuthal) magnetic field related to J. Finally lambda_visc is the viscous damping term and perhaps also the one that was the hardest to calculate without errors.

After many pages of calculations, we found the formula

with

for the magneto-static inviscid term. Assuming a badly conducting upper layer, we have

for the magnetic damping term due to the vertical imposed magnetic field, and here I_m are modified Bessel functions. For the viscous damping we find a two-term formula 

separating viscous damping due to dissipation in boundary layer on solid walls

from viscous damping due to dissipation in boundary layers that exist on both sides of the interface between both top and bottom liquids

The viscous damping rate formula compares well with experiments in orbital sloshing devices and many thanks to G. M. Horstmann for this extremely valuable input. 

Noticeable is that I initially got the viscous damping formula wrong allthough this was invisible in all the numerical and experimental tests that we had done. It learned me that dissipation in boundary layers at interfaces is not negligible and that factor two errors are hard to detect. Luckily, we were able to spot this error just inches before the paper got published. 

The level of detail reached by this new metal pad roll theory is extremely fine. In the following plot, we compare numerically measured growth rates (codes SFEMaNS & OpenFOAM) with the theoretical line, for simulations done in a tiny reduction cell (radius of 3.5 cm) with high imposed vertical fields (Bz = 16mT) and varying, high current densities

To get this totally unspectular plot right, we have literally needed months of work, in which we faced multiple turnarounds (and factors two) in theory and also some well hidden bugs in the numerical approach. Both codes SFEMaNS and OpenFOAM find sensibly the same results as predicted by the theory (be aware that this plot really zooms into the detail). No previous theory could have allowed us to reach this level of agreement.

The observed motion is the typical rolling motion of the interface, here one period decomposed in 8 snapshots from simulations done with SFEMaNS (using OpenFOAM, we get the same motion)

An unexpected but interesting side-product is that the same theory could also explain the growth rates in the simulation of the Mg-Sb battery done by N. Weber, as shows this plot 

This might seem surprising as liquid metal batteries have three layers, not two, but since Mg-Sb batteries have so heavy bottom layers that almost don’t move, metal pad roll instability behaves just as in a two layer system. Form our theory, we were also able to estimate that Mg-Sb batteries with more realistic sizes could become unstable under realistic conditions of current density (3kA /m^2) and ambient magnetic field (1 mT) when their radius exceeds values of about 30 cm. 

For us, it was extremily valuable to do this work, since it allowed to define a critical and physical benchmark for our numerical code SFEMaNS and OpenFOAM (for N. Weber). We just don't have so many metal pad roll theories that can withstand a quantitive comparison with numerical simulations. We hope that our theory can be picked up by other groups that also devellop multiphase MHD solvers and want to check them. 

The existence of a closed form analytical formula for viscous damping in two-layer systems is interesting for purely hydrodynamical experiments too. My collaborators G.M Horstmann and T. Weier from HZDR Dresden have used this new damping rate formula in a novel theory for orbital sloshing devices and this is currently under review.

This work published in JFM was one of the thoughest ones to finish and write down in my entire career. Certainly enough cylindrical coordinates, Bessel functions and perturbation methods for a few years. I thank our reviewers for having ploughed through these 49 pages and also know that I need to start writing shorter papers. 

Metal pad roll instability with liquid metals at room temperature 

Metal pad roll was first observed in realistic Hall-Héroult cells, but the chemical aggressive environment (operating around 1000° C, cryolite attacks almost every material) make it hard to conduct experiments there. Since then, engineers and scientists have been wanting to design a laboratory experiment in which the metal pad roll instability could be observed at room temperature. This necessarily demands to use different working fluids.  

Up until today, ony one research group (see these articles (1 and 2)  by A. Pedcenko et al.) has succeeded to build a device that can trigger metal pad roll instability at room temperature. In this set-up, GaInSn eutectic alloy  is used as bottom layer. The supposedly badly conducting top fluid layer is replaced by an array of thin steel needles. Metal pad roll instability is oberved with high imposed currents and for high imposed magnetic field. Quantitive comparison to existing theories remained difficult because of the steel wire array and because of lacking precise descriptions of viscous and magnetic damping of waves.

But why can’t we just stack two layers of liquid metals, liquid at room temperature, such as Ga over Hg for example ? This certainly is a question that several scientists have asked independently but the answer to that question is not so obvious.

Practically all the available metal pad roll theory is specifically designed for the case of a badly conducting cryolite, some 10000 times less conducting than the aluminium, bottom layer. When the conductivity jump is so high, the precise value of conductivity of both metals actually does not matter anymore and these material parameters, sigma_1 and sigma_2, vanish from the theory. This also means that we cannot use these theories to check wheter metal pad roll instability is possible with two well conducting metals. 
 
Our new MPR model is different in that aspect. As explained above, we find the destabilizing term in the growth rate as 

in which

is a conductivity dependent factor (mixed type top and bottom boundary conditions). This factor indeed asymptotes towards 1, when sigma_1 << sigma_2 and hence becomes independent of sigma_1 and sigma_2 as in all previous theoretical models. However, our model does offer the possibility to check other combinations of well-conducting liquid metals.

Around 2018, I started testing the possibility of metal pad roll with mercury and galium or galinstan. These tests were motivated by discussions with C. Gissinger (ENS Paris). Initial investigations suggested that huge electrical current densities (J) and magnetic fields (B_z) would be required to drive the metal pad roll instability, but now I know that this is mainly a consequence of a bad choice of system size. An experimental of about 10 cm in diameter indeed is out of scope as more than thousand of Amps would need to be sent through the liquids. This is technically difficult. However, in a smaller cell of 2 or 4 cm in diameter, MPR seems more easily reached.  

Early 2020, I started to explore the possibility of metal pad roll instabilty in a miscible metal-metal system, gallium (fluid 1) over GaInSn eutectic alloy (fluid 2). Allthough both liquids are miscible, we have a much smaller density jump than with gallium and mercury and there still is a weak difference in conductivity. Since our study on electro-vortex flows we also have a solver than can simulate the alloy and mixing of both liquids. According to theory, metal pad roll instability was possible, but only in small enough set-ups that are not larger than a few cm in radius. Simulations confirmed the theory.

While writing up these findings in a small article, I decided to look back into the gallium with mercury combination. Allthough the density jump is much higher, the conductivity jump is also higher with this pair of metals. The fact that we know explored small cells also changed a lot since we found that the gallium-mercury set-up could indeed destablize for almost similar values of current and magnetic field as in the galium-GaInSn eutectic set-up.

If this set-up is to be built as an experiment, don’t build it too large ! 

In a series of very challenging numerical simulations, we succeeded to confirm the predictions of the theoretical model. The following image shows a snapshot of the (turbulent) flow intensity and interface deformation in 2cm radius cell, filled with 2cm high layers of gallium and mercury. The imposed magnetic field Bz = 15 mT is certainly reachable with a pair of standard Helmholtz coils. The total electrical current sent vertically through the metals is significant here since some 377 A high, mainly for numerical reasons (the more unstable, the less time it takes for the wave to grow and numericall, shorter time = more economical to simulate). 

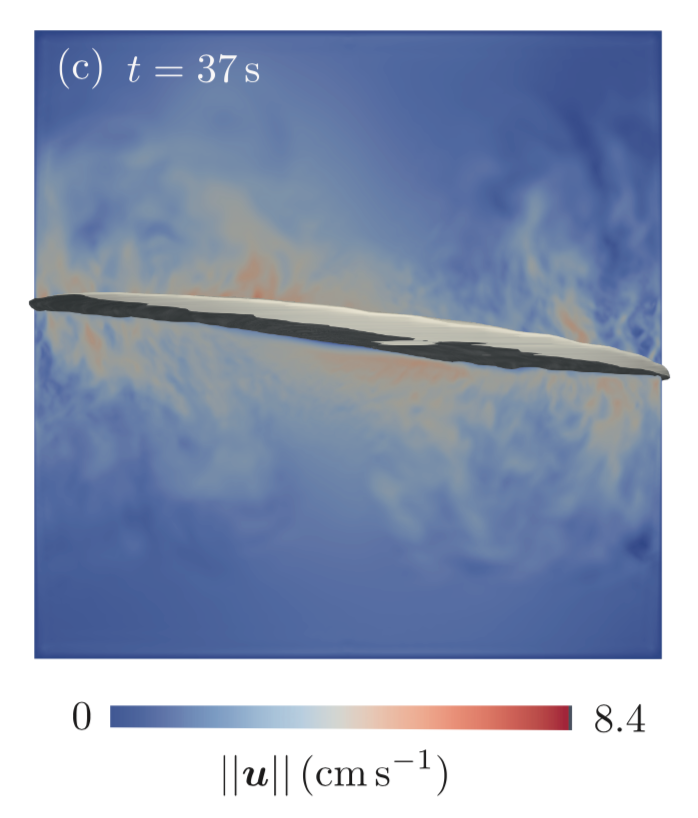
The numerical simulation of this mutliphase MHD flow took more than a week of massively parallel comptuations on the Jean-Zay cluster. It was only made possible by L. Cappanera's new multiphase algortihm. Despite the small size of the cell, this calculation is extremely challenging and this is due to the very thin viscous boundary layers (very fine spatial resolution, up to 0.08 mm scale), the high Reynolds number (Re up to 15000) and the essentially 3dimensional (turbulent) aspect of the flow. The fact that this was possible with SFEMaNS has bluffed me. 

Metal pad roll instabilty experiments with two liquid metals at room temperature are possible and only require a centimeter scale device. This is suggested by linear stability theory, but also confirmed by massively parallel simulations of the fully nonlinear, turbulent flow. We believe that this is an important message to send to the experimental MHD community, because many groups have the technical knowhow and material to build this type of small set-up.  This explains why we have sent this work as a letter to PRL (preprint here). This article is now published.

Three-layer theory for metal pad roll instability in LMBs 

The two-layer theory was an intermediate step to model metal pad roll instability in batteries, with three layers. With the help of a bright Master student, L. Wierzchalek, we finally managed to finish this three layer model. We basically extend the same perturbative method that was used in the two-layer system.

The main difficulty of the three-layer system is that gravity waves in three layer systems are more complex. For each azimuthal and radial wave-number, we have two different types of waves (slow and rapid) that may deform the interfaces. Depending on the density jump ratio

There is a preference for either slow or rapid waves. Using this theory, we can estimate when LMBs could become unstable in a worst case scenario (most unstable battery). We computed the critical current density as a function of system size, for different material combinations and using typical values for the thicknesses of the fluid layers. 

Here R, the horizontal axis is the battery radius. We can see that Mg||Sb batteries are the most easily destabilised. For this type of battery,  the maximal current density in protoypes was about 3000 A m^{-2}. This diagram tells us that in the worst case scenario, we could reach the onset of metal pad roll instability in a cell with radius of 0.5 m. LMBs that reach this scale do not yet exist. 

Next to this, we have also used our three-layer theory to explain the numerical observations of Horstmann et al. (2018). This study was published in JFM in 2023.