TAYLER INSTABILITY 

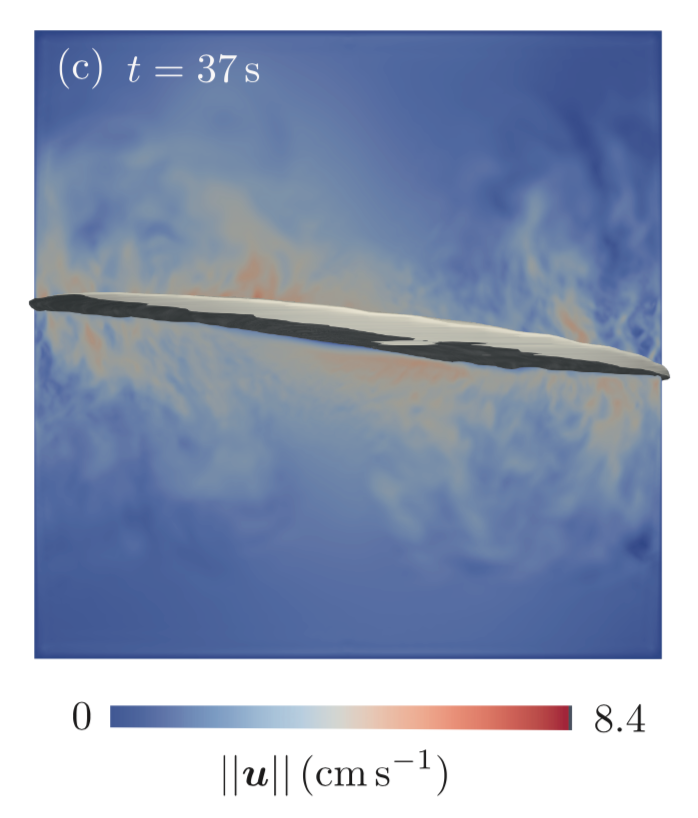
In 2015, we published a detailed study on the Tayler instability, combining theoretical analysis with direct numerical simulations. The Tayler instability was first studied in the 1960’s. Too intense electrical currents running through a conducting fluid at rest can magnetohydrodynamically destabilize. Flow then spontaneously emerge in the cell. In a homogenous (one phase) liquid metal column the flow (left) and the perturbed magnetic field density (right) look as 

Our simulations done with SFEMaNS confirm results obtained in previous studies (e.g. Weber et al., NJP 2014) and apply to low magnetic Prandtl number fluids. The flow has the structure of vertically packed, transverse rolls. The magnetic field perturbation is associated to redistribution of the electrical current density. We define the Hartmann number (Ha) and the magnetic Prandtl number (Pm).  

where mu0 is the vacuum permeability, J the current density, R the radius of the cell, sigma the conductivity of the fluid, rho its density and nu its kinematic viscosity.  Using linear stability analysis, we calculate the non-dimensional growth rate (gamma) of the instability for various Ha and Pm numbers

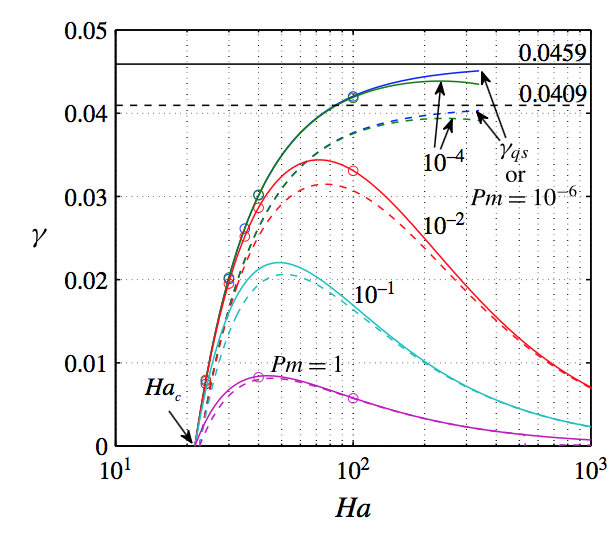
The data-points from direct numerical simulations (circles in the plot) compare very well with the theoretical curves. In realistic liquid metals with very low Pm, the theoretical curve (blue lines) grows monotonically with Ha and asymptotes towards the idealized quasistationary (qs) limit. The dimensional growth rate then scales as

Using simple weakly nonlinear arguments (supercritical bifurcation), we find that the dimensional magnitude of the flow can be estimated as

In LMBs, the Tayler instability is more complex to model due to the multiphase character of the cell. We expect that the instability can take place in either of the metal electrodes since there, the conductivity and so the Hartmann number is highest. Due to the lighter weight of the top layer, the instabilty will likely occur first in the top electrode.

Using the simple laws above for the growth rate and the order of magnitude of the Tayler-destabilized flow, we make some estimates to provide a suggestive answer to two questions

1. at which size R the battery will become Tayler unstable ?  
2. at which size R the Tayler instability can become so intense that it can disrupt the thin salt layer ? 

Taking into account that current density J is not unlimited in batteries, we make a phase diagram for the critical radius Rc beyond which a cylindrical LMB would become unstable. We plot this critical radius as a function of the aspect ratio h=H/R where H is the cell's height. 

Cells are unstable above the coloured lines that refer to different typical maximal current densities (i) 3 kA/m^2, (ii) 10 kA/m^2 and (iii) 100 kA/m^2. Taking the green curve (ii) as a reference J=10kA/m^2, we can expect Tayler instability in batteries with radii larger then Rc =0.23 m. This is quite a big battery: none of the existing LMB prototypes reached this size. 

To estimate when Tayler instability may disrupt the salt layer, we use a simple energy criterion. The kinetic energy density that is available due to Tayler instability needsto exceed  the potential energy density needed by a fluid particle in the top layer to pinch through the electrolyte layer. This leads to the criterium 

for ‘’safe’’ electrolyte layer heights He.  In the formula, we find the densities of the top and salt layers, g is gravity. Using the formula for the dimensional flow magnitude Udim, we calculate the estimated minimal safe electrolyte layer height for the three typical different current densities (i) 3 kA/m^2, (ii) 10 kA/m^2 and (iii) 100 kA/m^2, and plot it as a function of battery size R:

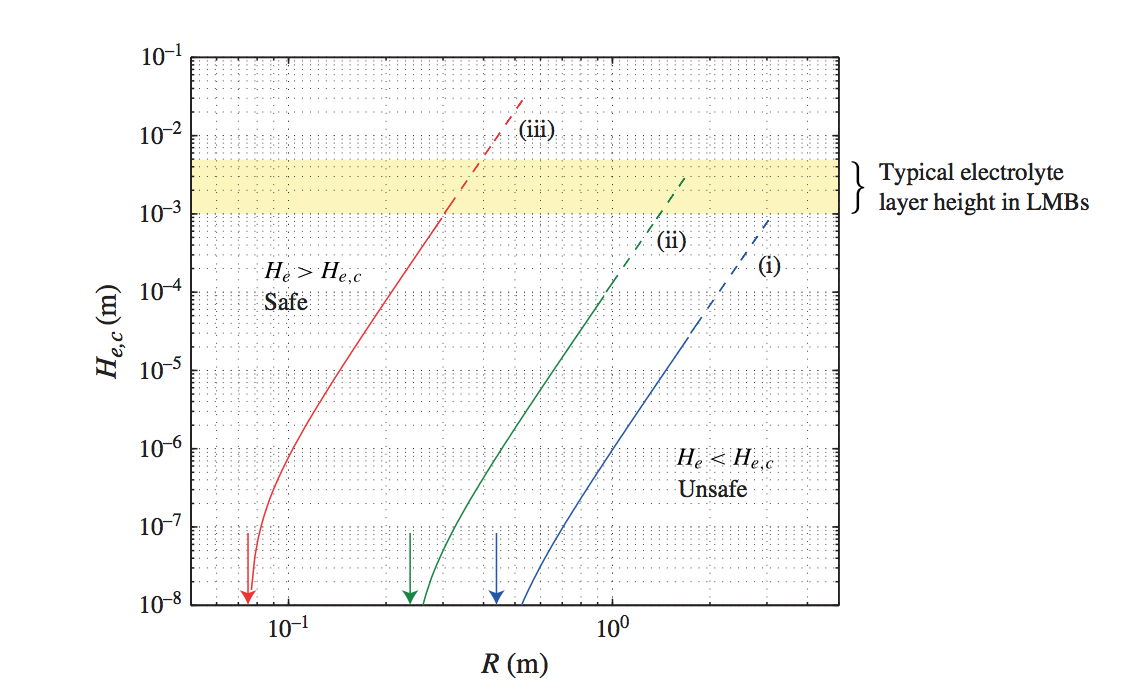
Batteries are unsafe to the right of the coloured lines. Vertical arrows locate the critical radii of the Tayler instability threshold. From this plot, we can read when the curves reach the yellow band that highlights the 1 mm - 5 mm  range of typical electrolyte layer height. Taking (ii) J= 10 kA/m^2 as a reference value, we thus estimate that Tayler instability may become intense enough to disrupt the thin electrolyte layer in batteries that are as large as  R> 1.4m. This is quite a big battery and suggests that Tayler instability can’t generate very violent flows in LMBs. 

The direct numerical simulation of a Tayler destabilized LMB is a numerically challenging task, in particular when one wants to use realistic values for the material properties. In our article, we have done some multiphase simulations for artificial parameter regimes, in order to explore whether the criterium we propose for battery-safeness  is useful. The following graph show a Tayler destabilized cell in micro-gravity (g is artificially low) for increasing Hartmann number (increasing current density or radius)